
Inhalt
Die allgemeine Prämisse der titelgebenden Kreatur in Angriff auf Titan: Flügel der Freiheit ist, dass sie Menschen sind vergrößert und meist sinnlos. Einige haben keine Haut, was sie grausamer macht, aber das ist nicht das einzige, was sie anders macht als andere, die Riesen sind. Sie haben einen unersättlichen Appetit auf Menschen. Und diese Kreaturen sind der Grund, warum in der Überlieferung des Spiels drei riesige Mauern um die Stadt errichtet wurden. Sie sind der ganze Grund für die 3D-Manövrierausrüstung, die ich letzte Woche erwähnt habe. Und wenn wir ehrlich zu uns selbst sind, sind sie der Grund, warum wir uns für das interessieren Angriff auf Titan Franchise in erster Linie.
Viele Leute haben bereits über die Wissenschaft der Riesen gesprochen, und ich werde auf jeden Fall noch einmal darüber sprechen, da es äußerst wichtig ist, die Physik hinter Riesen zu verstehen und warum bestimmte Tiere so groß werden wie sie und andere nicht. Meine eigentliche Absicht in diesem Artikel ist es jedoch, eine andere Frage zu beantworten: Wie groß kann ein Titan realistisch werden? Lassen Sie uns also noch einmal die Scheiße herausfinden Angriff auf Titan: Flügel der Freiheit.
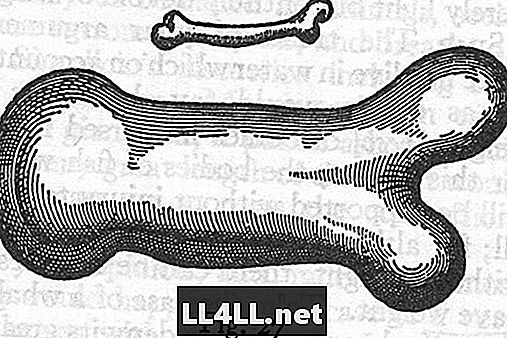
Galileo sagt
Wir haben alle von Galileo gehört, richtig. Der Typ, der oft in den Himmel starrte. Nun, er war bekannt für mehr als seine Astronomie. Er war tatsächlich ein genialer Mathematiker. Außerdem war er ein erstaunlicher Beobachter. In seinem Buch Zwei neue Wissenschaftenspricht er über zwei Schiffe, beide sind in jeder Hinsicht identisch. Vom Mast bis zum Deck und vom Bug bis zum Heck gab es keine Unterschiede außer einem: Einer ist doppelt so groß wie der andere. Er stellt fest, dass das größere Boot mehr Gerüste und Stabilisierung erfordern würde, damit es nicht unter seinem eigenen Gewicht zusammenbricht.
Aber das macht doch keinen Sinn, oder? Es ist nur größer. es sollte die gleichen physikalischen Eigenschaften haben wie etwas, das kleiner ist, oder? Leider ist diese Behauptung falsch. Auf einer fundamentalen Ebene sind die Atome in jedem der Objekte gleich, aber es gibt mehr Atome im größeren Objekt, aber auf einer praktischeren Ebene ändert sich die Geometrie mit dem größeren Objekt.
Stellen Sie sich einen Würfel vor, der 1 cm mal 1 cm groß ist, ein Volumen von 1 cm³ oder 1 l hat und mit Wasser gefüllt etwa 1 g wiegt. Wie viel Wasser würde ein 10-cm-Würfel enthalten? Wenn Sie 10 cm³ oder sogar 100 cm³ denken, liegen Sie falsch. Es würde 1.000 cm³ fassen. Zusätzlich hat sich die Masse proportional auf 1.000 g verdreifacht. Dies nennt man Galileos Quadratwürfelgesetz.
Ein Titan hat menschliche Proportionen, ist aber ungefähr 15 m groß. Wenn der durchschnittliche Mensch ungefähr 1,5 m hoch ist (siehe, wohin gehe ich damit?), Ist ein Titan 10-mal so groß wie er. Abgerundet wird das Durchschnittsgewicht eines 1,5 m schweren Menschen auf 70 kg. Dies bedeutet, dass ein menschlich geformter Riese, der zehnmal so groß ist wie er, die 1.000-fache Masse und 70.000 kg wiegt. Das sind übrigens 70 Tonnen. Ohne eine zusätzliche Stützstruktur würde ein Titan unter seinem eigenen Gewicht zerdrückt werden, ganz zu schweigen von der Kraft, die er benötigt, um so viel Blut durch sein System zu pumpen.
Nebenbei bemerkt, wenn Sie einen Titan in den Nacken schneiden, sprudelt Blut. Sie erkennen, dass wenn Ihr Charakter mit diesem Strom von Körperflüssigkeiten getroffen würde, es wäre, als würde man mit einem vollständig geöffneten Feuerwehrschlauch getroffen.

Galileo sagte in seinem Buch: „Schließlich können wir sagen, dass für jede Maschine und Struktur, ob künstlich oder natürlich, eine notwendige Grenze festgelegt ist, die weder Kunst noch Natur überschreiten können. hier versteht sich natürlich, dass das material das gleiche ist und der anteil erhalten bleibt. “mit anderen worten, es gibt eine strukturelle begrenzung für alles. Was sind die Grenzen des menschlichen Körpers? Ich werde mich wegen der Anzahl der beteiligten Variablen an den Rahmen halten und nicht an das Kreislaufsystem oder ein anderes System wie dieses, aber ich weiß, dass viele dieser Schwellenwerte viel niedriger sind als die interne strukturelle Integrität. Wir arbeiten hier wahrscheinlich mit dem Best-Case-Szenario.
Der größte Mann, der jemals gelebt hat, wurde in Alton, IL, geboren, nur einen Katzensprung von meinem Elternhaus in St. Louis entfernt. Sein Name war Robert Wadlow. Er stand volle 8 Fuß 11 Zoll (2,7178 m). Über einen Meter größer als der Durchschnittsmensch. Und obwohl er sehr dünn war, wog er 220 kg, mehr als das Dreifache eines durchschnittlichen Menschen. Wadlow musste sogar spezielle Hosenträger an seinen Beinen tragen, um ihm zusätzliche Unterstützung für seine Masse zu geben. Leider starb Wadlow im Alter von 22 Jahren an den Folgen seiner Größe.
Galileo postulierte, dass die Knochenstruktur für etwas, das doppelt so groß ist wie ein Mensch, ungefähr viermal so dick sein müsste. Er malte sogar ein Bild von einem Beinknochen. Es gibt jedoch nach wie vor Probleme mit der Verwendung dieses Stoffes in einem Titan, wenn man die Belastungsgrenze des Knochens im Allgemeinen betrachtet.
Ein menschlicher Knochen hat eine Festigkeit von ca. 4.400 MN / m², dh wenn der Druck über dem Knochen mehr als 4.000 NM beträgt, wird er zerkleinert. Ein durchschnittlicher Mensch übt im Stehen 55 MN / m² oder im Gehen 110 MN / m² auf seine Knochen aus, nicht schlecht. Aber ein Titan mit einem Gewicht von 70 Tonnen würde 110.000 MN / m² bringen, wenn wir ein einfaches Verhältnis hätten.
Realistisch, Ein Titan könnte wahrscheinlich nicht viel größer sein als Wadlow, ungefähr 3 Meter, aber wo ist der Spaß dabei? Lassen Sie mich wissen, was Sie in den Kommentaren denken, und lassen Sie mich wissen, was passiert, wenn Sie die Scheiße daraus herausfinden.
