
Inhalt
- Zipfs Gesetz erklärt
- Grundlegendes Experiment
- Zipfs Gesetz in Steam-Märkten
- Was können wir über Steam lernen?
- Schlussfolgerungen
Vor kurzem schlug ein Freund vor, ich solle mir Vsauces-Video über Zipfs Gesetz, Paretos Prinzip und ihre mysteriösen Erscheinungen um uns herum ansehen. Hier ein kleiner Vorgeschmack, der Ihre Aufmerksamkeit erregt: 80% aller Menschen leben in 20% der beliebtesten Städte. 80% aller Grundstücke gehören 20% der reichsten Grundbesitzer; 80% aller Abfälle befinden sich in den obersten 20% der mülligsten Straßen - wie nach dem Gesetz von Zipf und dem Paretos-Prinzip vorausgesagt.
Nicht genug? Nun, wie ich gestern herausgefunden habe, hört das Kaninchenloch hier nicht auf ... Voller Skepsis beschloss ich, mir anzusehen, wie viel Zeit die Leute mit Steam-Spielen verbringen ... Nun. 80% der Zeit der Menschen wird damit verbracht, 20% der beliebtesten Spiele zu spielen ... Interessant? Nun, lesen Sie weiter, es gibt mehr zu dieser Geschichte.
Mit über 20 Minuten ist Vsauces Bestreben großartig und erklärt eine Menge der wichtigen Dinge über Zipf. Er ist jedoch sehr schüchtern, wenn er uns den Kernmechanismus zeigt, von dem allgemein angenommen wird, dass er dazu beiträgt, warum Zipf so funktioniert. Bevor wir fortfahren, möchte ich dies kurz erläutern.
Zipfs Gesetz erklärt
Es gibt verschiedene konzeptionelle Möglichkeiten, um die Intuition hinter dem 20/80-Prinzip zu erklären. Das beste Beispiel ist meiner Meinung nach das über Mondkrater.
Grundlegendes Experiment
Stellen Sie sich also vor, es gäbe einen unberührten Mond - eine vollkommen glatte Oberfläche. Nehmen wir an, es gibt einige zufällig große Asteroiden, die den Mond wohl oder übel treffen. Wenn der erste Asteroid landet, verlässt er einen Krater. Jetzt trifft ein anderer und hinterlässt einen Krater an anderer Stelle. Jeder Krater ist ein Teil der Gesamtfläche, daher besteht die Möglichkeit, dass der nächste zufällige Asteroid in der Nähe eines vorhandenen Kraters auftrifft und sich mit ihm zu einer Gruppe zusammenschließt. Die Wahrscheinlichkeit, dass ein neuer Asteroid auf einen bestimmten Krater trifft, ist dann proportional zur Größe der vorhandenen Krater und Asteroiden. Dies bedeutet, dass der nächste zufällige Asteroid eher der größten bestehenden Gruppe beitritt und diese sogar noch größer macht. Eine Art kumulativer Prozess, der dann einen Mechanismus schafft, der reich, reich, arm, einsamer macht.
Denken Sie daran, denn das ist vermutlich die allgemeine Erklärung dafür, warum das Zipfs-Gesetz mit solch mysteriöser Universalität arbeitet. Das Beispiel eines Asteroiden ist recht einfach, die Frage ist jedoch, was bei vielen Wiederholungen passieren wird
Ein bisschen verwirrend?
Nun, ich habe ein GIF gemacht, um diesen Anfangspunkt nach Hause zu fahren. NB! Die Grafik wird später besprochen. Versuchen Sie einfach, sich das Experiment vorzustellen.

Wenn wir den tatsächlichen Mond beobachten, stellt sich heraus, dass die beobachteten Kraterdurchmesser mit zunehmender Anzahl von Asteroiden so zunehmen, dass sich die oberen 20% der größten Krater 80% der gesamten Oberfläche nähern.
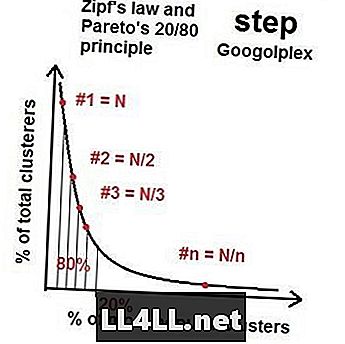
Wenn wir uns also mehr Asteroiden zuwenden, nähert sich die Verteilung der beliebtesten auf die am wenigsten beliebten Gruppen mit dieser 20/80-Eigenschaft einer Art "idealer Verteilung" - einer Pareto-Verteilung. Wenn Sie rechnen, stellt sich heraus, dass (im Allgemeinen) wenn die größte Gruppe die Größe N hat, die zweitgrößte Gruppe um die Größe N / 2 liegt, die dritte N / 3 und so weiter und so fort. Dies nennt man das Zipf-Gesetz. Das Seltsame ist, dass Zipfs Law- und Pareto-Verteilung für eine verwirrende Menge von Elementen (Asteroiden) und Gruppen (Kraterhaufen) funktioniert. Natürlich gibt es Verzerrungen und zufällige Störungen, aber der allgemeine Trend ist nicht zu leugnen.
Ich hoffe, Sie können sehen, wie Asteroiden, die mit größerer Wahrscheinlichkeit große Krater auf dem Mond treffen, eine Verbindung zu Städten herstellen, die attraktiver sind, wenn bereits mehr Menschen in ihnen leben. Man muss jedoch erkennen, dass Städte weit entfernt von den einzigen "Gruppen" sind, die sich laut Zipf verhalten.
Hier einige Beispiele von Mark Newmans Forschungen zu Pareto-Distributionen. NB! Die Diagramme haben eine logarithmische Skalierung, die die hyperbolische Form der Kurven glättet und eine nahezu lineare Beziehung darstellt.
Anfängliches y = aX ^ (- b)
Logs beider Seiten => log y = log a - b log X
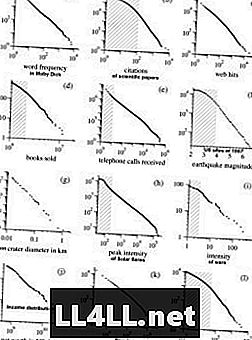
Interessanterweise zeigt sich der gleiche Trend auch bei religiösen Kulten ... Die gemeinsame Eigenschaft der meisten dieser Phänomene ist einfach diese Tendenz "große Gruppen werden größer". Das Gesetz von Zipf besteht also in Mechanismen, in denen die Präferenzen von Elementen positiv mit der Gruppengröße zusammenhängen (dh je größer die Gruppe, desto wahrscheinlicher wird sie wachsen). Deshalb stelle ich mir Gruppen gerne als Cluster und Elemente als Clusterer vor.
Zipfs Gesetz in Steam-Märkten
Misstrauisch gegenüber dem letzten? Hier sehen Sie, wie viel Zeit die Nutzer für die beliebtesten Steam-Spiele aufwenden. Daten von SteamSpy.
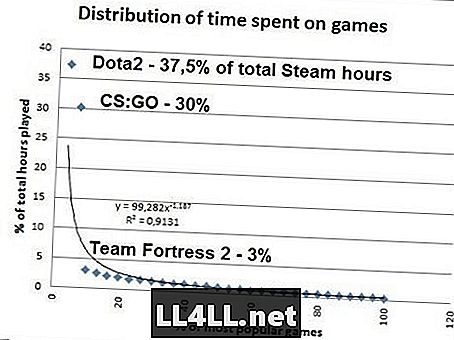
Wenn Sie rechnen, stellt sich heraus, dass 20% der beliebtesten Steam-Spiele 80% des gesamten Spiels ausmachen, so dass das Pareto 20/80-Geheimnis hier wie ein Zauber wirkt ... Man muss jedoch beachten, dass für Zipf um wahr zu sein, CS: GO muss 37,5% / 2 = 18,8% der Gesamtzeit ausmachen, anstatt satte 30%. Aber abgesehen von diesem Ausreißer (STOP PLAYING CS: GO) ist die Zipf-artige Distribution eindeutig da.
Hier sehen Sie die Anzahl der verkauften Exemplare für die beliebtesten Spiele.
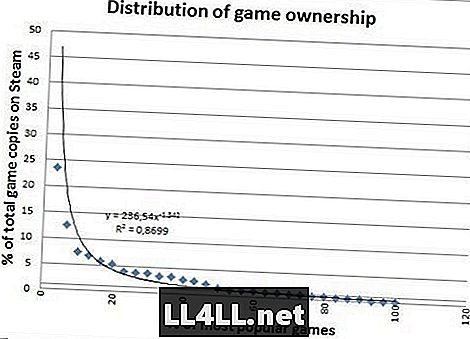
Sieht viel besser aus, oder? Die verkauften Exemplare weisen keine großen Ausreißer auf, daher passt sie sehr gut, was ein bemerkenswerter Unterschied ist. Aus den Unterschieden der letzten beiden Grafiken lässt sich jedoch noch etwas Interessanteres schließen.
Bemerken Sie, dass der "Schwanz" nach rechts im zweiten Diagramm etwas fett ist? Nun, in einfachen Worten, das zeigt uns, dass die "relativ unbeliebten" Spiele tatsächlich sehr viel beliebter sind als in der vorherigen Handlung.
In der Tat stellt sich heraus, dass 20% der beliebtesten Spiele nur 60% des Umsatzes ausmachen, gegenüber 80% beim Spielen. Interessant? Wetten, dass es dein Arsch ist?
Was können wir über Steam lernen?
Nun, die Tatsache, dass die Popularität des Spiels der Pareto-Distribution folgt, zeigt, dass es tatsächlich eine Art positiven Netzwerkeffekt gibt, der die Spieler dazu bringt, Spiele auszuwählen, die bereits von mehr Leuten gespielt werden. Der Unterschied im Fettgehalt von Schwänzen ist, dass Steam-Nutzer beim Kauf von Spielen viel mehr "gruppengrößenblinde" sind als beim Spielen.
Denken Sie darüber nach - je mehr Leute Spiele kaufen, ungeachtet der "aktuellen Meinung der Bevölkerung", desto weniger verbreitet sich die Pareto-Distribution, da es weniger wahrscheinlich ist, dass große Spiele weiter wachsen. Wenn niemand einen Rattenfuss darüber gab, wie viele Leute bereits ein Spiel spielen und die Verfügbarkeit aller Spiele gleich war, würden wir davon ausgehen, dass 20% der beliebtesten Spiele etwa 50% des Umsatzes und der Spielzeit ausmachen (z. B. unter der Annahme, dass individuelle Vorlieben vorliegen) normal verteilt).
Schlussfolgerungen
Es gibt also zwei Faktoren, die zur Pareto-Verteilung in Steam-Märkten beitragen - wie innovativ die Entwickler sind (wie viele neue Mondkrater werden gebildet) und wie sehr die Spieler (Asteroiden) die aktuelle Gruppengröße schätzen, wenn sie sich für eine Gruppe entscheiden . Wie sich herausstellt, sind Gamer beim Kauf von Spielen sehr gruppengrößenblind, aber im Gegenteil. Cool was?
Wenn Sie mehr über die Verteilungen von Zipf Law und Power Law erfahren möchten, finden Sie hier einen schönen Vortrag. Schauen Sie sich auch unbedingt Newmans Artikel an!
Wenn Sie mehr von dieser Art von Material lesen möchten, werde ich bald genug versuchen, diese Beobachtung mit einem Modell zu verbinden, das zeigt, dass populärere Multiplayer-Spiele höhere Preise haben (was auf die Präferenz von Spielern verweist, größeren Gruppen beizutreten). Siehe den Artikel hier. In dem Artikel Piece De Resistance wird versucht, diese Theorien zusammenzuführen und zu erläutern, wie Multiplayer-Spiele, soziale Netzwerke und Städte in Wirklichkeit allesamt konkurrierende Güter mit Netzwerkeffekten sind (je mehr Menschen ein Gut konsumieren, desto mehr profitiert jeder einzelne Verbraucher) betitelte sie mit diesem Zipfian Nebel des Geheimnisses ...
Bis dahin - amüsiert euch!
P.S. Fügen Sie einen Kommentar mit einer lustigen Idee für eine 20/80 Beziehung ein, von der Sie glauben, dass sie wahr ist.
Meine sind:
80% der Nostalgiker werden durch 20% ihrer glücklichsten Erinnerungen verursacht (tatsächlich bewiesen für die Rate, bei der Menschen Informationen vergessen).
80% der Masse sind in 20% der größten Weltraumobjekte konzentriert (tatsächlich nachgewiesen für die Verteilung der Gravitationskraft)
Und natürlich
80% der Unordnung in Ihrer Toilette kommt von 20% von dem, was Sie essen (keine akademische Forschung zu sprechen)